이분 탐색 문제이다. 이전 문제들과 마찬가지로 중간값 검증을 어떻게 할 것인지, 범위를 어떻게 할지 가장 중요했다.
이분 탐색으로 내가 찾고 싶은 값은 만들어진 구간의 최소 값이다. 즉 중앙값을 기준으로 구간을 만들 때 문제에서 원하는 구간 개수가 가능한지 검증한 후, 더 적게 나온다면 문제에서 원하는 구간 개수를 만들 수 있다는 뜻이므로, 최솟값을 찾기 위해 중간값을 줄이고, 더 많이 나온다면 중간값을 올리는 과정으로 문제를 해결하였다.
다시 정리하자면, 내가 원하는 값(중앙값)으로 구간을 나눌 때 M개 이하로 만들 수 있다면, 내가 정한 값으로 M개의 배열을 만들 수 있다는 것을 확실히 인지하여야 한다. 이를 이용하여 중앙값을 검증할 때, 내가 지정한 중앙값으로 배열의 최소 최대의 최대 차를 만들 수 없는 숫자가 나온다면, 구간을 새로 하나 씩 추가하는 과정으로 검증하였다.
코드로 살펴보자면,
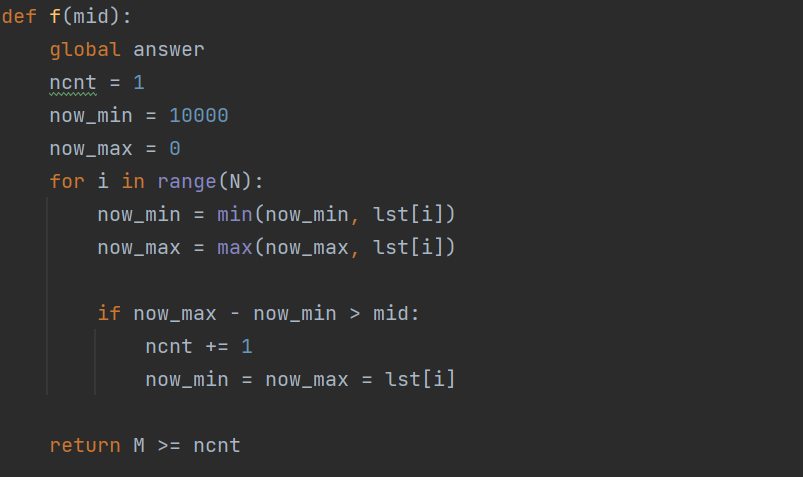
이렇게 된다.
1번 TC를 살펴보자면, 만약 mid 가 6인 경우 [1,5,4,6,2,1,3,7] 이렇게 하나의 최소 최대 차가 6인 배열을 만들 수 있다.
이 배열을 임의로 조정한다면 [1,5,4], [6,2], [1,3,7] 4,4,6점으로 총점수가 6점(mid) 값인 배열을 만들 수 있다. 하지만 6보다 더 작은 경우도 가능할 수 있기 때문에 검증을 더 해봐야 한다.
mid가 4인 경우를 보자면 [1,5,4], [6,2], [1,3], [7] 이런 식으로 구간을 나눌 수밖에 없다. 이 경우에는 어떻게 임의로 조정하더라도 구간의 개수가 3이고, 점수가 4점인 배열을 만들지 못한다.
마지막으로 mid가 5인 경우를 보자면 [1,5,4,6,2,1,3], [7]의 배열을 만들 수 있고 이 배열을 임의로 조정하여 [1,5,4], [6,2,1], [3,7]로 문제 조건을 만족시킬 수 있다.
즉, 여기서 검증은 중간값을 기준으로 배열의 개수를 최소로 만들었을 때, 그 개수가 M이하인 경우 중앙값이 더 작아도 가능한지 검증하는 것이다.
중간값을 검증하는 코드만 완성한다면, 이진 탐색 코드는 금방 짤 수 있을 것이다.
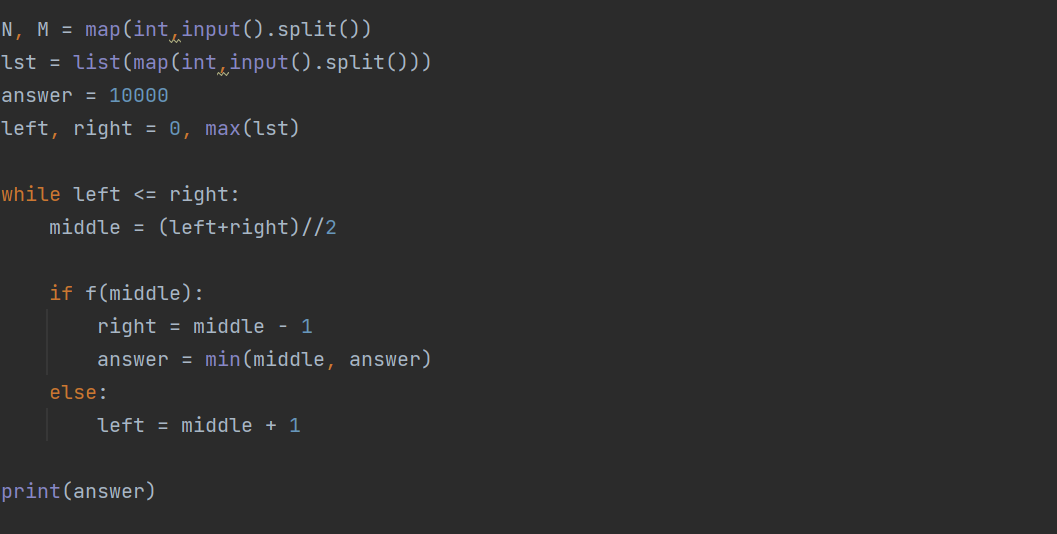
백준의 Code_plus의 이진 탐색(연습) 문제들을 풀고 있는데 말만 연습이고 난이도는 연습이 아닌 것 같다.
'알고리즘' 카테고리의 다른 글
| [PROGRAMMERS] 힙(Heap) : 디스크 컨트롤러 Python (0) | 2022.06.07 |
|---|---|
| [백준] [이분탐색] K번째 수 : 1300 Python (0) | 2022.06.06 |
| [백준] [이분탐색] 기타 레슨 : 2343 Python (0) | 2022.06.04 |
| [PROGRAMMERS] 연습문제 : 야근지수 Python (0) | 2022.06.03 |
| [백준] 플로이드 : 11404 Python (0) | 2022.06.01 |
