이 문제는 무지와 어피치가 출발점 S에서 택시를 타고 가는데 둘이 각자의 집으로 갈 때 최소 택시요금을 구하는 문제이다. 여기서 둘이 공통된 방향으로 택시를 타고 갈 때는 합승이 가능하다는 추가 조건이 있다.
이 부분까지 읽었을 때 다행이 내 머릿속에 바로 다익스트라가 떠올랐다. 다익스트라 알고리즘이란 그래프 경로 간에 가중치가 있는 경우, 한 꼭짓점에서 다른 꼭짓점 간의 최단 경로를 찾는 알고리즘이다. 나는 이 문제를 보고, 각 목표점(꼭짓점)과 그 사이를 이동할 때 택시요금(가중치)의 최단 택시요금을 구하는 점에서 다익스트라로 충분히 구현 가능하다고 생각했다.
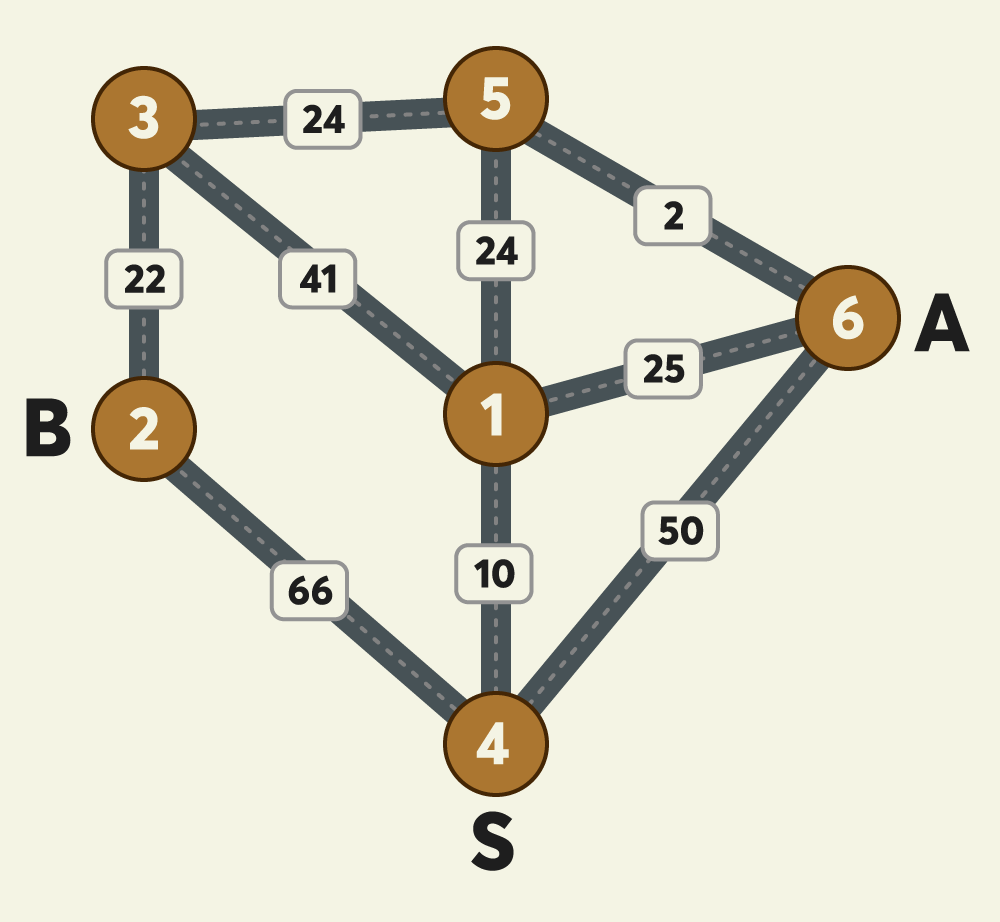
하지만 이 문제를 풀기 위해서 추가로 고민했던 점이 있다.
1. 이 문제는 효율성 테스트도 점수가 있다. 시간/공간 제약을 정확히 명시해주지는 않았지만 고려할 필요가 있었다.
2. 단순히 시작점에서 A와 B로 가는 최단 요금의 합이 아닌 합승을 고려한 최단 요금의 합을 구하여야 한다.
처음 문제를 접근할 때, 시간제약이 무서워 다익스트라를 기반으로 그리디 한 방법으로 접근을 해보았다.
1. A-B의 최단요금 구한다
2. 최단거리를 추적하여 어떤 노드가 최단거리인지 확인한다
3. 시작점에서 최단거리까지 거리 중 가장 가까운 요금을 찾아 1과 더하여 답을 낸다.
예제 TC를 위 방법으로 했을 때, 답이 나오는 것을 확인했지만 답을 제출했을 때, 예외사항이 있는지 오답이 나왔다. 역시 그리디로 문제를 풀려고 하는 것은 위험한 풀이였다. 하지만, 답을 제출하면서 확인한 것은 다익스트라 알고리즘 자체가 시간이 많이 걸리지 않는다는 것이다. '그렇다면 다익스트라를 기반으로 완전 탐색을 풀어도 시간 통과를 할 수 있지 않을까? '라는 생각으로 다시 접근했다.
1. 모든 꼭짓점을 돌면서 S, A, B 까지의 최단 요금을 구한다.
2. 그 중 최솟값을 답으로 반환한다
이를 코드로 구현한다면,
from collections import deque
def solution(n, s, a, b, fares):
def my_bfs(num):
v1 = [max_value] * (n + 1)
Q = deque([[num,0]])
v1[num] = 0
while Q:
now, nsum = Q.popleft()
for i in range(1,n+1):
if arr[now][i] and v1[i] > arr[now][i] + nsum:
v1[i] = arr[now][i] + nsum
Q.append([i,v1[i]])
return v1[s] + v1[a] + v1[b]
max_value = 100000 * n
arr = [[0] * (n+1) for _ in range(n+1)]
# 인접 행렬을 이용하여 그래프 저장
for x, y, f in fares:
arr[x][y] = arr[y][x] = f
return min([my_bfs(i) for i in range(1,n+1)])N의 최댓값이 200이므로 조금 걱정했지만, 그래도 구현 자체는 어렵지 않기 때문에 금방 제출했고 다행히 통과됐다.(시간제한이 어느 정도 인지 모르겠지만 간당간당했을 것 같다.)
조금 어려웠던 문제였지만, 다익스트라 알고리즘을 알고 있는 사람이라면 쉽게 풀었을 거 같다.
오늘도 하루 한개 알고리즘 파이팅!!
문제 출처 : https://programmers.co.kr/learn/courses/30/lessons/72413
'개발' 카테고리의 다른 글
| [Python] heaqp 라이브러리를 이용한 우선순위 큐 (0) | 2022.06.02 |
|---|---|
| [SSAFY] 1학기 최종 프로젝트 : 영화 추천 사이트 (0) | 2022.05.28 |
| [Python] collections.Counter : 딕셔너리 서브 클래스 (0) | 2022.05.15 |
| [Python] re 라이브러리를 이용한 정규표현식 (0) | 2022.05.07 |
| [PROGRAMMERS] 월간 코드 챌린지 시즌 1 : 쿼드압축 후 개수 세기 Python (0) | 2022.05.02 |
